las cuatro escalas

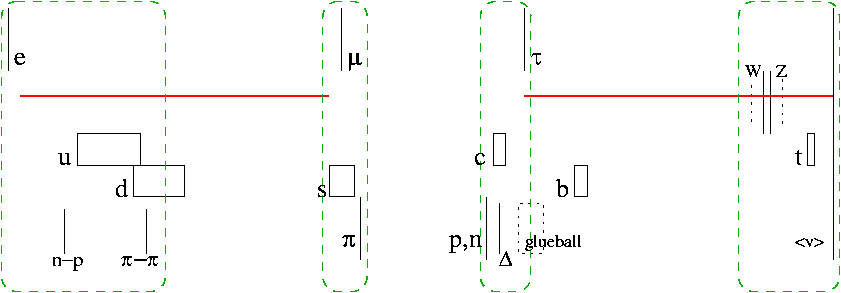Para los que visitan este blog por cuestiones de fisica de particulas, he aqui ploteadas, a escala logaritmica, las principales masas del modelo estandar. Estando como estan, intexplicadas, no deja de ser sorprendente la forma en la que se agrupan, en cuatro niveles bien reconocibles:
A)la ruptura electromagnetica (con esas diferencias de masas debidas a carga electrica)
B)la ruptura quiral (donde va a parar el pion)
C)la escala de QCD (donde va a parar la glueball, ie el gap de SU(3) )
D)la ruptura electrodebil

Uno podria imaginar el ir conectando poco a poco las interacciones. Primero SU(3) con solo gluones, que cae en el area (C). Luego arrancamos los fermiones de SU(3) y nos aparece el pion, que en principio deberia ser un Goldstone, de la ruptura quiral, sin masa pero se echa para arriba a la zona (B). Y si conectamos ahora SU(2) electrodebil o U(1) electromagnetica, nos aparecen las otras dos escalas. Por otro lado podriamos empezar conectando primero el grupo electrodebil y ver que va saliendo. Lo curioso de toda esta historia es que las distintas generaciones no tienen obligacion alguna de ajustarse a estas escalas, pero mas o menos lo hacen, y con espectacular precision en el caso del muon y el tau.

En rojo he pintado el factor correspondiente a la cte de estructura fina. Entre muon y electron hubo en tiempos articulos justificandolo. Entre tau y el vacio electrodebil fue sugerencia de un amateur, Jay R. Yablon, hace poco. En todo caso la simetria entre las particulas es tan alta que se explica uno el que encajen muchas formulas empiricas buscadas a ojo (me he ahorrado de momento el pintarlas aqui).

1 comentario

[Anónimo - 28 de mayo de 2005 - 19:02]

Este dibujico lo he incluido en un articulo para el arxiv, hep-ph/0505220, en el que le dabamos vueltas a otra rareza de los leptones cargados: que parecen presentar cierta logica cuando en vez de la masa se considera, uff, las raices cuadradas (!) de la masas como si fueran componentes de un vector.

La raiz cuadrada de m era un componente tipico en la frecuencia de un oscilador y de ahi incluso en campos no relativistas, eq de ondas etc. Pero deja de tener su uso con relatividad, donde c nos permite un viaje mas comodo de energias a frecuencias (y de energias a velocidades). Quizas en un producto de discreto por continuo todavia pudiera tener sentido darle uso a la raiz de m.